Stefano Pezzano

Postdoctoral researcher

Cerfacs

CFD team

Welcome!

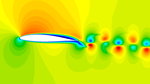
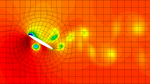
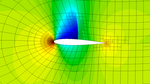
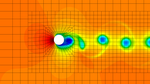
My name is Stefano and I am a postdoctoral researcher at Cerfacs in Toulouse. My research focuses on advanced numerical methods for fluid mechanics for aerospace applications.

Interests

High-order numerical methods for PDEs
Isogeometric Analysis
Mesh Generation, Refinement and Deformation
Computational Fluid Dynamics
Large Eddy Simulation

Education

PhD in Applied Mathematics, 2021
Université Côte d'Azur - Inria
MSc in Aerospace Engineering, 2018
Politecnico di Torino
BSc in Aerospace Engineering, 2015
Politecnico di Torino

Experience

Postdoctoral researcher

Cerfacs

Oct 2021 – Present Toulouse, France

Scale resolved simulation of turbulent flows using high-order Discontinuous Galerkin schemes in the context of the Nextsim project.

PhD Fellow

Acumes team, Inria

Oct 2018 – Sep 2021 Sophia-Antipolis, France

Development of a Discontinuous Galerkin solver for compressible flows with moving boundaries, using a high-order geometry representation derived from Computer Aided Design. The proposed methodology is implemented in the open source platform Igloo.

Supervisor: Régis Duvigneau

Predoctoral Research Fellow

Memphis team, Inria

Apr 2018 – Sep 2018 Bordeaux, France

Development and validation of an immersed boundary solver for turbulent flows on parallel octree grids. Application to aeroelastic simulations of wind turbine blades.